问题描述
直线拟合是数据挖掘中最最最基本的算法之一了,如果给定一群点,让你直接用一根直线去拟合,那么这就是最基本的线性回归问题。但是如果给定如下一群点,这群点里可能存在多根直线需要拟合呢?
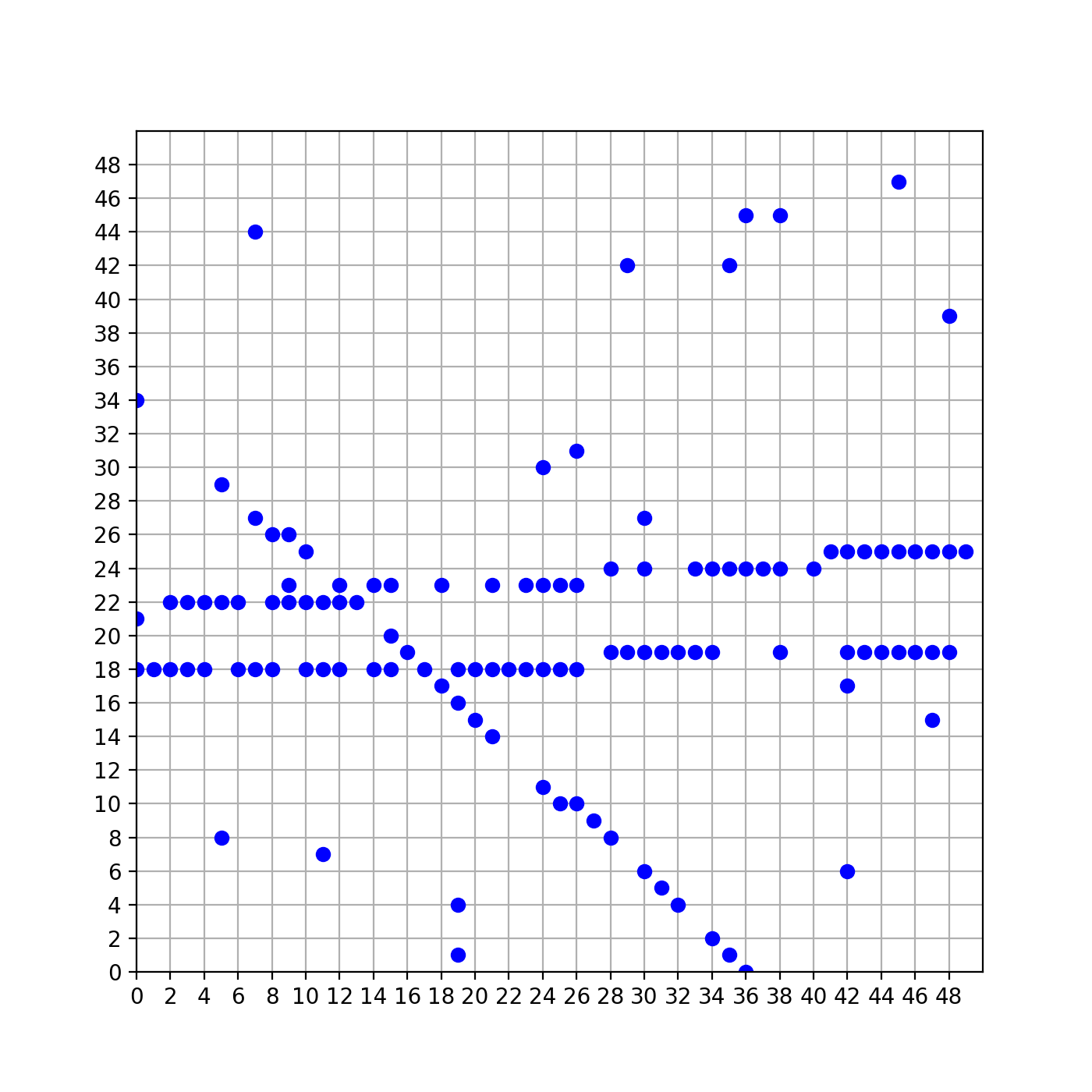
此时显然无法用线性回归直接求解了,因为我们根本不知道哪些点是属于哪根直线的。
求解思路
暴力求解法
基本思想
先说一种最暴力的方法,既然我们的目的是找出那三根直线,那不如先把所有可能直线枚举出来。然后在这些直线中进行筛选,得到结果。这里就涉及到了两个问题:
- 如何枚举直线
- 如何进行筛选
首先对于第一个问题,最容易想到的方法就是把所有数据点进行两两组合(两点可以确定一根直线)得到所有可能的直线,然后对这些直线进行筛选。
然后在筛选阶段,我们又会碰到两个问题:
- 何如判断一根直线的比另一根好?
- 由于是使用数据点两两组合生成的直线,不可避免的会生成许多重复的直线(这里的重复指的是直线的方差跟截距差得很小),如何对这些直线去重?
这两个问题都可以用一个方案来解决,那就是计算一下一根直线大概穿过了哪些点。我们可以设置一个阈值 $d$ 来解决这个问题,只要点到直线的距离小于这个阈值,我们就认为该直线穿过了这个点。
那么对于每一条直线,我们都能计算它穿过了哪些点。我们把直线 $l$ 穿过的点的集合记作 $p_l$。很容易想到,对于两条直线 $l_1, l_2$ 如果 $\vert p_{l1}\vert > \vert p_{l2}\vert $,那么 $l_1$ 更可能是我们需要拟合的直线。同时,如果 $\frac{\vert union(p_{l1}, p_{l2})\vert }{min(\vert p_{l1}\vert , \vert p_{l2}\vert )} > \gamma$,我们就认为这两条直线是重合的,这里 $\gamma$ 是另一个超参数。
所以最后我们只要根据每条直线的 $\vert p_{l}\vert $ 进行排序,并对排序后的结果去重,最后留下的直线就是我们需要拟合的了。
复杂度分析
这种暴力求解的方法时间复杂度是 $O(n^3)$,所有点两两组合为 $O(n^2)$,然后对于每条线需要过一遍所有的点,计算哪些点在直线上,所以最后的复杂度是 $O(n^3)$。
优化方案
当然这里还有一定的优化空间,比如对于任意两点,如果它们的距离大于某个阈值,我们就不去计算这两点所生成的直线了。
基于 KMeans 聚类的直线拟合法
基本思想
回想一下,暴力求解法效率低下的问题在于,其根据所有点两两的组合生成了 $\frac{n(n-1)}{2}$ 条直线,而这些直线中,大部分都是没有用的。那么我们能不能在这一步用一种更好的算法先进行一步筛选,过滤掉大量的无意义的直线呢。
再回想一下,当我们使用两个点去计算一条直线的时候,我们实际上得到的是一条线的截距和斜率。对于在同一条直线上的点,它们之间的两两组合应该拥有相近的截距和斜率才是。如果我们把截距和斜率看做一个二维空间里的点,这个二维空间实际上就是直线的特征空间,里面的每个点都代表了一条直线。
因此,根据所有数据点的两两组合,我们可以生成它们对应在直线特征空间里的一个点,然后对这些点进行聚类,聚出来的几大类应该就会是我们需要拟合的几条直线了。
但事情并没有这么简单,我们可以先看一下特征空间中数据的分布图(横坐标是斜率,纵坐标是截距,都已经归一化):
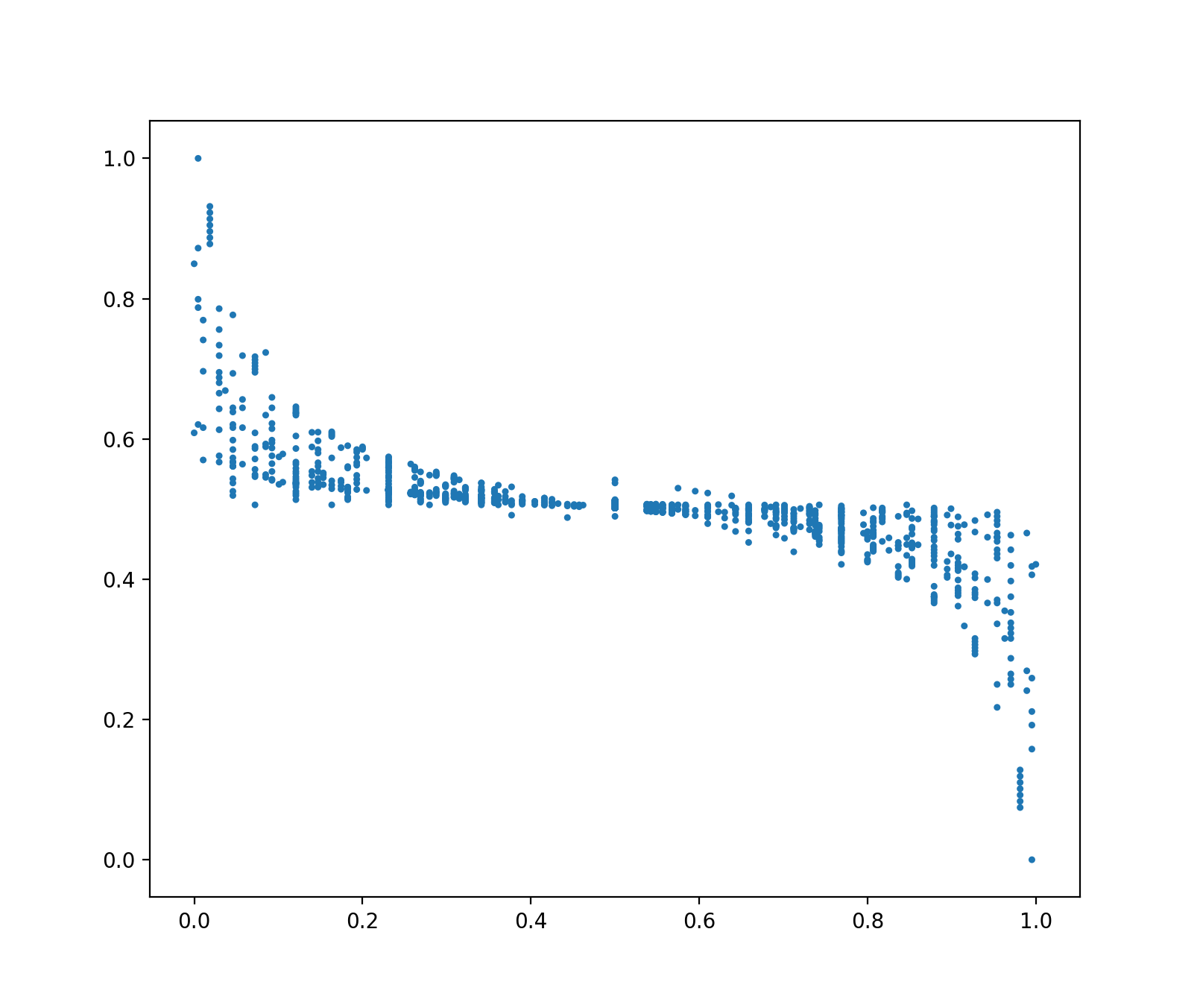
它并没有随三条直线聚集成明显的三类,反而分布得比较稀疏。所以想根据这些特征空间里的点直接聚出三类来是不大可能的。为了更直观的理解这些特征空间里的点,我们还是对其先进行一个大致的聚类,然后在原始空间中看看聚类的效果:
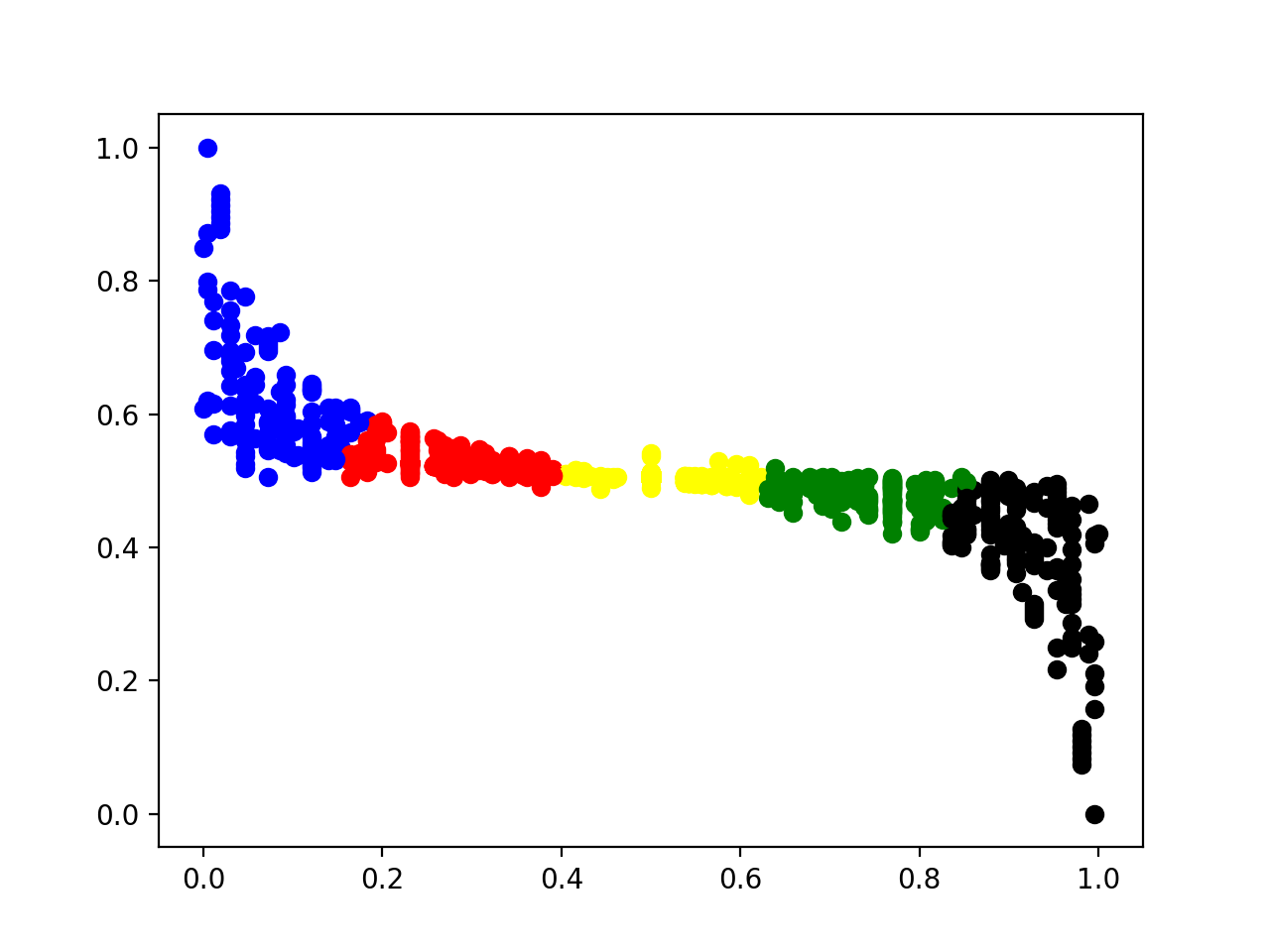
这里我首先试了一下聚成5类,可以看出,聚类还是基本有效的,但是也存在着很大的问题,比如中间两条水平线,就被聚到同一个类别中。尽管我在这里已经用了上一节最后提到的小 trick ,先过滤了很多线,但是依旧存在噪音点过多的的问题,使得最后的聚类效果不佳。
既然直接把这三根直线聚出来是不太现实的,那么我们能不能退一步,把聚类的数量增大,使得聚类的粒度变小,让中间这两根水平线能够区分开来。而对于同一个直线上的一对一对的点,我们有理由相信它们是能够聚起来的,毕竟它们之间的相似度总得比噪声强吧。
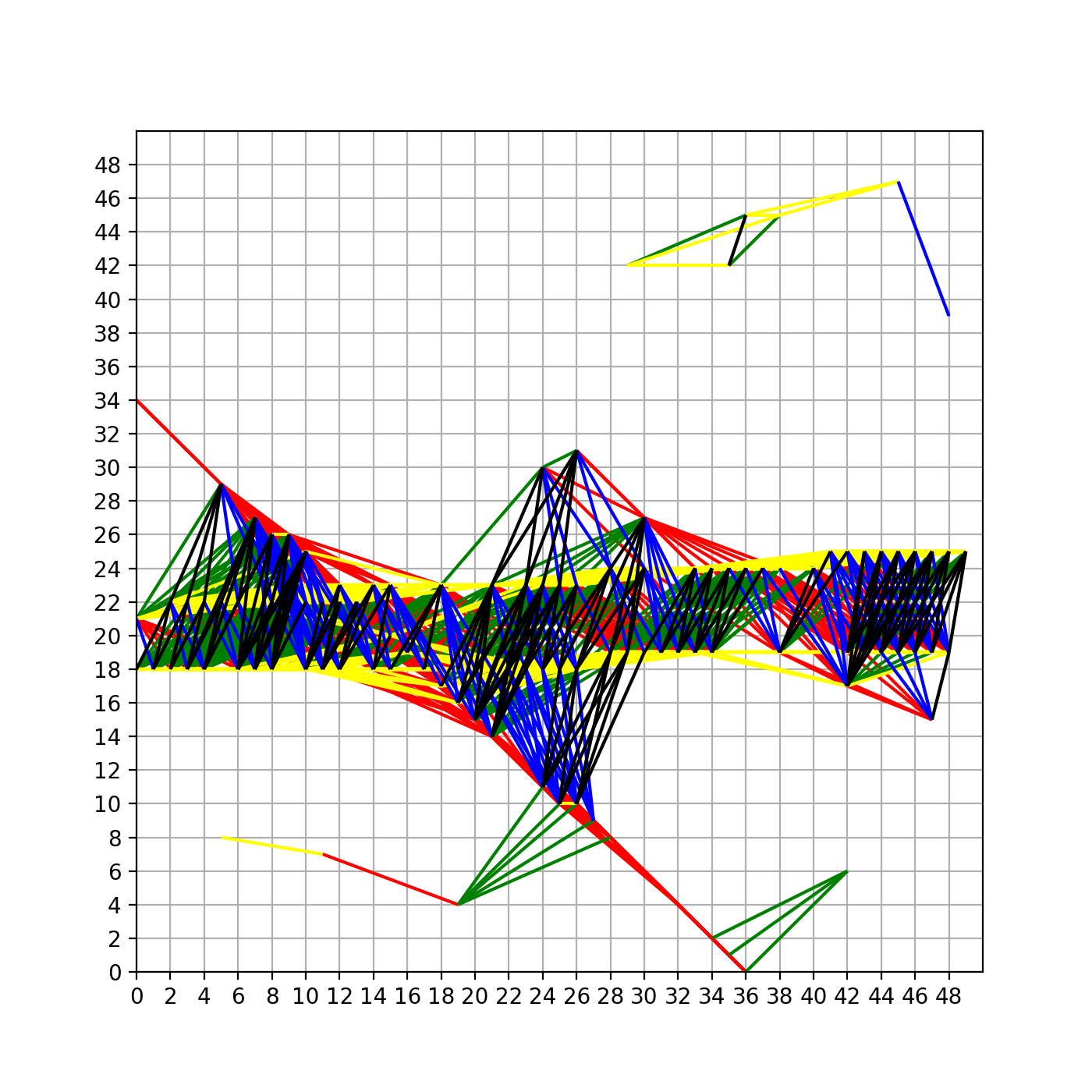
所以我之后把聚类的个数设置成了40,聚类完毕后再回到原始空间画出这些结果,如下图:
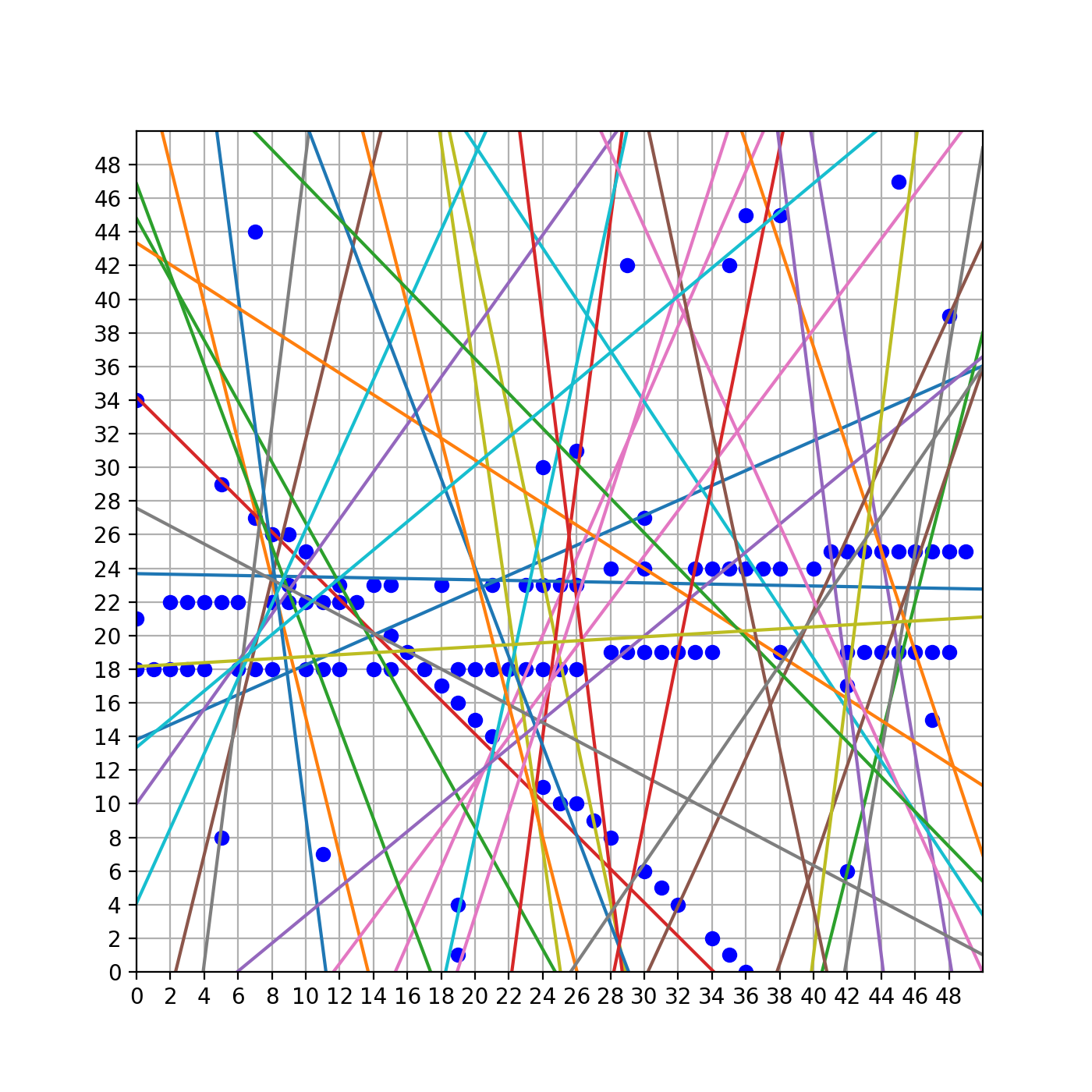
可以看到,在我们得到的这所有的直线中,是有直线大致穿过了那些需要我们拟合的点的。因此我们剩下的工作就是把这三条直线找出来,找的方法在上一节已经介绍过了,就是排序加去重。
当然,这里用聚类得到的结果并不是我们最终需要的,从图中也可以看出来这些直线并没有很精准的穿过那些数据点。因此,对于筛选完后的直线,还需要根据其本身穿过的那些点做线性回归,再重新计算其穿过的点,如此迭代得到更为精确的结果。
那么最后的结果如下:
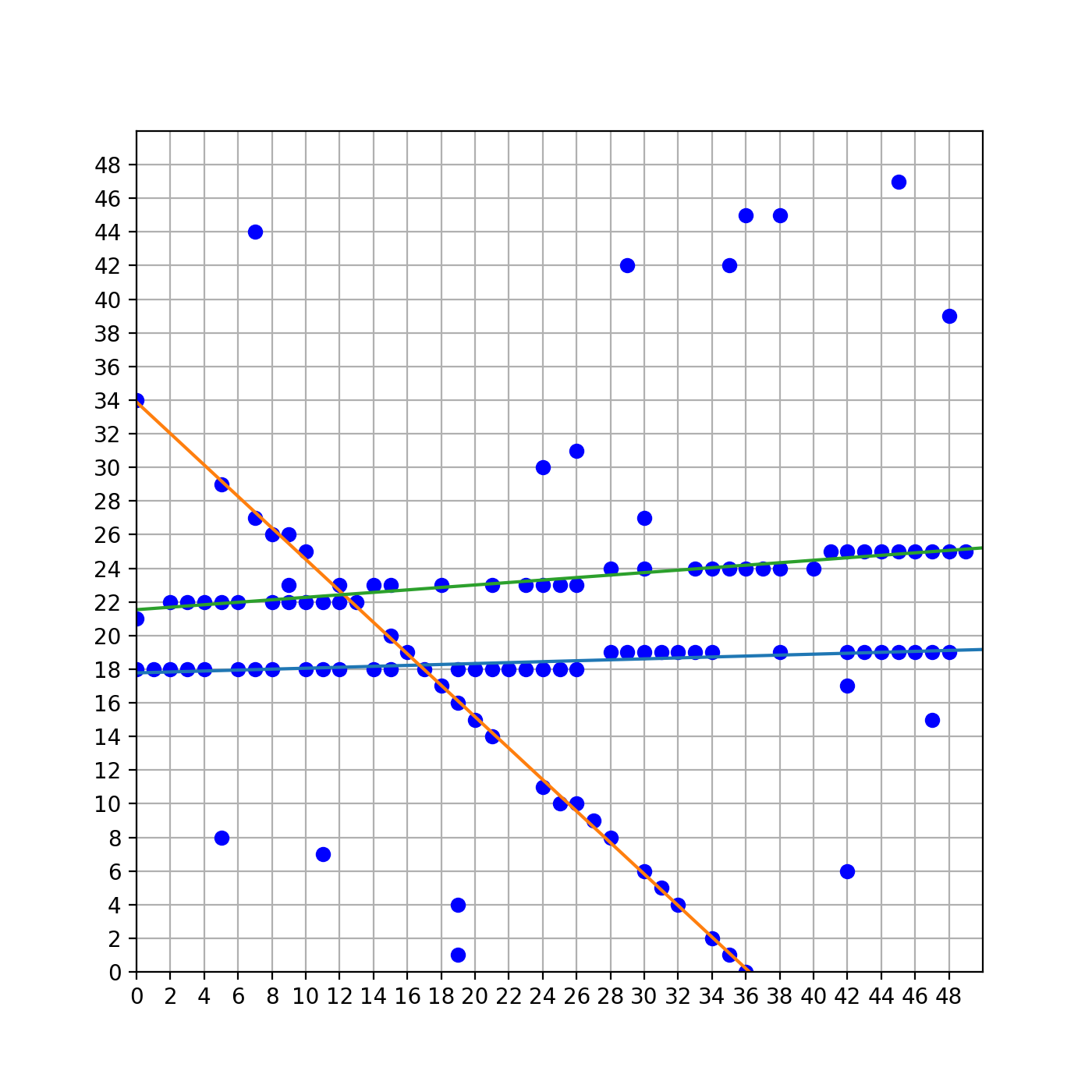
复杂度分析
首先还是需要所有点的两两组合,复杂度为 $O(n^2)$,然后进行 KMeans 聚类,时间复杂度为 $O(knt)$,$t$ 为迭代次数。最后是直线的筛选,复杂度为 $O(k^2)$
后记
在实现基于 KMeans 的算法中,由于自己的不小心踩了特别多的坑,比如在聚类之前没有进行数据预处理(归一化),导致中间的结果非常奇怪。好在这个问题可视化非常方便,使得可以顺利地解决bug。但以后一定要多加小心注意才是。
总得来说这是一个很有意思的问题,所以才想写下这篇帖子。最后要特别感谢妹子 yukiho 跟我分享并且讨论这个问题,没有和你的头脑风暴估计都不会想到第二种方案~