基于神经网络的语言模型
对于基于神经网络的语言模型 neural networks based language models, 所占计算比重最大往往是 softmax 之前的大矩阵乘法. 如隐层大小为 $h$, 输出词表大小为 $V$, 那么其计算复杂度为 $O(hV)$, 随 $V$ 的增大呈线性增长.
要想提升模型的效率, 必须在这块上做出改进. 改进的方向主要有两种:
- softmax-based approaches
- sampling-based approaches
前者比较出名的方法有 hierarchical softmax, differentiated softmax. 后者的代表方法有 Noise Contrastive Estimation. 文章 有对这些方法的一个很棒的综述, 包括了比较详细的理论分析.
我写本文的目的主要是为了对之前自己做的一部分工作进行总结, 会比较详细的介绍 Factorized Softmax 的工程实现细节, 和在实现过程中碰到的各种各样坑.
Factorized Softmax
理论
Factorized Softmax 实际上是 hierarchical softmax 的一种简化版本, 可以看做一个 two-layer hierarchical softmax. 它首先将词语分类, 每个词语都只属于一个类别(当然也可以分配给多个类别, 这种情况本文先不讨论). 因此各个类别之间是互斥的. 词语概率公式的计算则如下:
其中 $w$ 是目标词, $c$是目标词所属类别, $h$ 是隐层向量. 实际上等式右边的两个概率都是通过 softmax 实现的, $p(c|h)$ 是对所有的类别进行 softmax, $p(w|c, h)$ 是对c类里的所有词进行 softmax.
如果我们将整个此表划分为 $d$ 个类别, 每个类有 $V / d$ 个词语 (平均划分). 那么上述公式的计算复杂度为 $O(hd) + O(h V/d)$, 容易看出, 当 $d = \sqrt{V}$ 时计算复杂度最小 $2O(h\sqrt{V})$
工程实践
理论上, 我们将 $O(hV)$ 缩减到了 $2O(h\sqrt{V})$, 这是一个很大的提升. 但实际实现过程中, 提升的比例没有理论上那么大, 原因是多方面的, 但其中最重要的一点是: 现在的神经网络训练都是以 batch 为单位的!!!
standard softmax 计算伪代码如下:
hidden : (b * h)
out_embed : (h * V)
out_bias : (V)
dot_value = hidden * out_embed + out_bias
p_words = softmax(dot_value)
其中 $b$ 是 batch size, 在上面的代码中, 每个数据都需要计算所有 output words 的概率, 所以将 hidden 直接与 out_embed 相乘, 得到的矩阵每一行代表一个时刻的 output words 的 score, 再进行 softmax 得到概率分布.
factorized softmax 能减少运算量的关键点在于, 其将每个词对应的 out_embed 给缩小了, 因为在训练语言模型的过程中, 我们是知道 target word 的. 因此我们只需要计算 target word 对应 class 的概率以及这个 class 内的 output words 的概率分布即可. 但问题也随之而出, 由于 hidden 的每一行都对乘上不同 out_embed , 那么也就没法用一个简单的矩阵乘法来实现了.
我的实现思路很直接, 如下图所示:
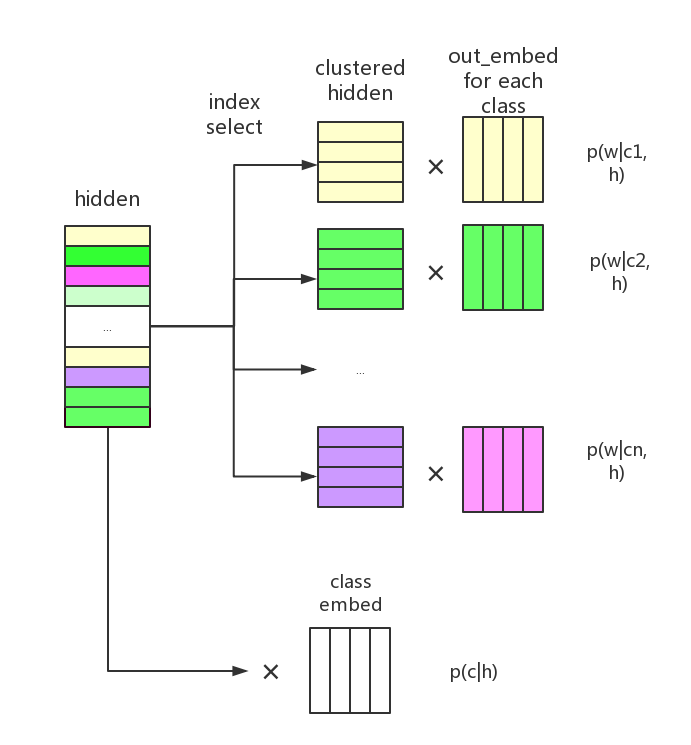
就是通过 index_select 操作, 将在同一个 class 内的 hidden 给聚集起来, 这样聚集后的 hidden 就能够直接与其对应类别的 out_embed 相乘, 得到这个 class 下的 target words 的概率分布 $p(w|c, h)$. 实际上, 如果我们想求得一个词最终的概率, 还需要将 $p(w|c, h)$ 与 $p(c|h)$ 相乘. 而我们在之前的 index_select 操作中, 已经将 batch 里数据的顺序打乱了, 因此实际上计算 $p(c|h)p(w|c,h)$ 并不是那么方便. 幸运的是, 在实际训练过程中我们可以忽略这一步. 循环神经网络语言模型训练的目标是:
不失准确性, 我们可以对其取对数:
在 factorized softmax 中, 训练准则如下:
也就是说, 我们可以分别计算 class 和 word 的 loss, 最后加起来就行了, 可以省去计算每个词概率的步骤.
这种做法简洁直观, 但也有相对应的 overhead . 要完成上述操作, 我们需要 build 一些额外的 label . 首先是 index_select 这一步的 index . 我们需要知道在当前 batch 内, 哪些 index 是属于哪个 class 的. 也就是说应该有一个 index_dict , key 是 class, value 是当前 batch 里属于这个 class 的 index. 此外, 在计算 $p(w|c,h)$, 我们需要知道 target 实际上是词语 $w$ 在 class $c$ 内的 within index, 所以还需有一个 target_dict 来记录每个 class 的 within index.
经测试, 在实际训练过程中, 构建这两个 dict 的开销是很大的, 而且因为它们的内容跟 batch 的内容高度相关, 因此也不方便提前计算. 在ptb语料上测试, 10k词表, 构建这两个 dict 所花的时间和神经网络 forward 的时间基本相当, 因此这个 overhead 可以算很大了.
一个失败的优化方案
我现在想到的方案是采用2个进程, 一个进程用来构建数据, 另一个进程用来神经网络计算. 采用 producer-consumer 的模式, pytorch 里也有支持 multiprocess 的 package. 所以改起来还是比较方便的. 进程间的通讯使用 Queue , 在 pytorch 的 multiprocess 里, 放入 Queue 的 tensor 是会自动存入 shared memory 中的, 所以在传给另一个进程时可以省去复制的操作. 但是每次传 tensor 时会有个固定的开销, 这个开销与 tensor 的 size 无关. 所以在实际使用过程中, 这个方案就变得不适用了. 因为我的 dict 里有很多个 tensor (有多少个 class 就有多少个 tensor). 这些 tensor 叠加起来所产生的开销甚至比我直接计算它们的开销还大.
但是我认为这种双进程 producer-consumer 的模式还是很适合神经网络训练的, 相当于神经网络在 forward-backward 的过程中可以同时开始计算下个 batch 所需要的数据. 在一些 build batch data 所需时间较长的模型中比价适用.
总结
目前我的结果是在 6W 词表的数据集上, 比 standard softamx 能缩短1/4的时间, 显存的使用量能减少一半, PPL相当. 词表更大的话加速比也应该会更好. 当然这个加速比还远远不够. 代码开源在了 github上.
虽然 factorized softamx 在理论上能够极大的减少计算量, 但实现过程中的诸多不便也是其现在没有多少工作继续跟进的主要原因. 日后我也会继续优化模型, 寻找更好的解决方案.