前言
最近一直在看一些传统机器学习算法,相比深度学习,传统计算学习算法的理论基础比较扎实,各种分析也更为透彻,往往一些基础简单的算法背后有着各种各样有意思的联系,比如 SVM 与 LR 的区别只是在于损失函数略有不同,而 LR 实际上是最大熵模型的一种特殊表现形式。因此在这里详细总结一下最近的这些感悟。
线性分类器
分类问题是机器学习中最基础的一个问题,其中线性分类问题更是万物之源。我们先来考虑二分类问题:给定数据点${x_1, x_2, …, x_n}$, 以及它们的类别 ${y_1, y_2, …, y_n}(y \in {1, -1})$,如何找到一个超平面 $y = W^Tx+b$,能将这两类点分隔开来。为了简便,我们用 $\theta=[W;b],x=[x;1]$, 因此有 $y=\theta^Tx$。当 $\theta^Tx > 0$时,我们认为这个数据点属于类别 $y=1$,反之亦然。
进一步想,我们可以认为 $|\theta^Tx|$ 是模型对数据点 $x$ 给出的打分,也是$x$距离超平面的远近,可以表示预测的确信程度。而 $\theta^Tx$ 的符号与标记 $y$ 符号是否一致能表示分类是否正确,所以可以用 $\gamma = y\theta^Tx$来表示分类的正确性和确信度,这也是函数间隔的概念。
对于线性分类器来说,我们模型的参数 $\theta$ 已经确定了,剩下的问题是如何定义一个函数来描述这个参数 $\theta$ 的好坏(这就是损失函数),以及如何针对损失函数找到最合适的 $\theta$ 具体数值(这就是优化算法)。本文主要讨论损失函数,优化算法不做详细展开。
逻辑回归与SVM
逻辑回归(LR)
逻辑回归(logistic regression, LR)是一种常用的分类算法,可以用作二分类也可用作多分类,多分类实际上就是 Softmax。我们在这里先讨论二分类的情况。
逻辑回归本质上是一种线性分类器,它的目标就是找到一个超平面 $W$ 来最小化它的对数损失函数,具体定义如下:
逻辑回归的公式可以统一为:
其对数似然函数为:
最大化对数似然等价于最小化损失函数:
通常我们还会加上 L2 norm 来提升模型的泛化性能:
其中 $\gamma_i = y_i\theta^Tx_i$ 是我们之前提到过的函数间隔,这个值大于0说明分类正确,值越大说明确信度越高,小于0说明分类错误,值越小说明错误的确信度越高。
SVM
SVM本质上也是一种线性分类器,但它的优化准则与逻辑回归不同。注意函数间隔 $\gamma$ 是可以随着 $W$ 的大小而成比例改变的,但是成比例改变 $W$ 是不会影响超平面的位置的。所以我们定义几何间隔 $\frac{\gamma}{||W||}$ 来消除这种影响。函数间隔与几何间隔的区别如下图:
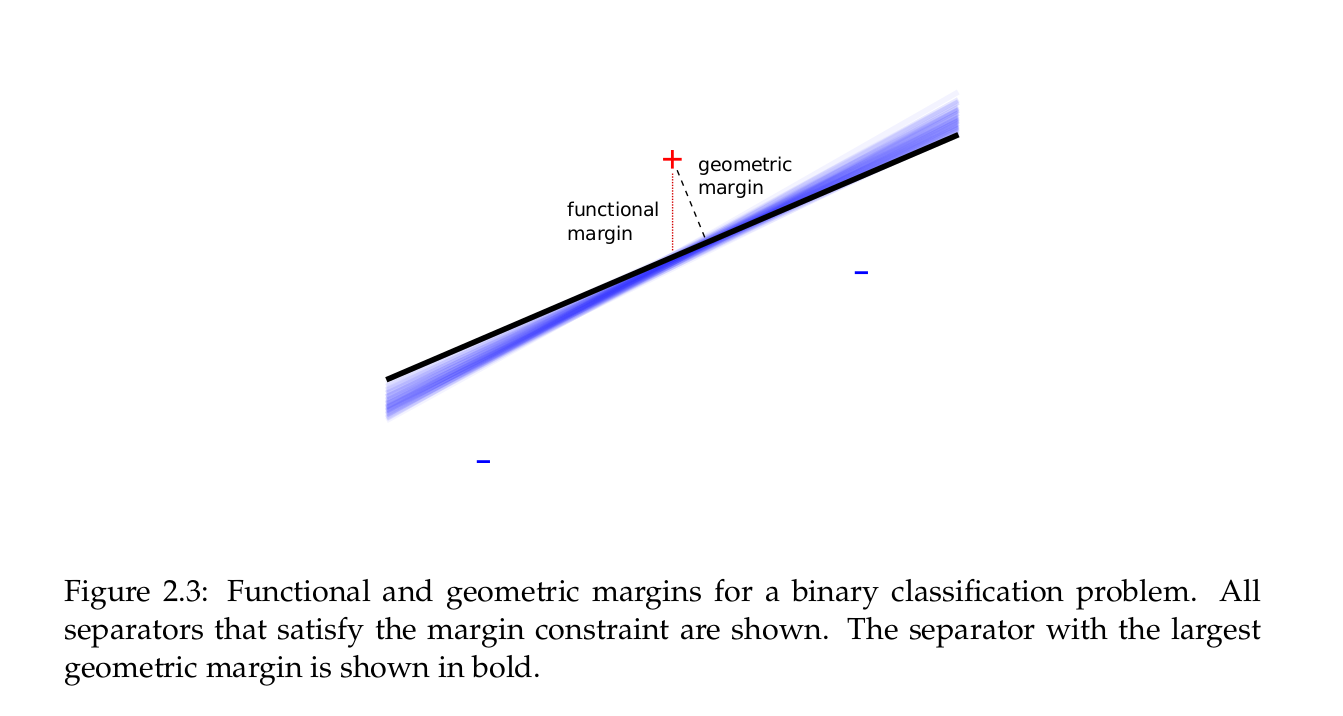
SVM 的优化目标则是在保证所有样本分类正确的情况下,最大化所有数据点里最小的几何间隔:
其中 $\hat{\gamma} = \min_{i=1,…,n} \gamma_i$。实际上,$\hat{\gamma}$的取值并不影响最优化问题的解(因为我们可以成比例缩放参数 $\theta$ 的大小),为了方便计算,我们可以取 $\hat{\gamma} = 1$,由此原问题变为
等价于:
在以上推断中,我们都认为数据是完全线性可分的,所以才能满足条件 $y_i\theta^Tx_i \ge 1$。但实际大多数情况中,数据是不完全线性可分的,因此我们需要加入松弛变量 $\xi$,使得优化目标变为条件变为:
松弛变量的意义在于,我们允许数据出现一定误分情况,但误分情况越严重($\xi$越大),惩罚越大。由上式两个条件,我们可以将松弛变量表示为 $\xi_i = max(0, 1 - y_i\theta^Tx_i)$,因此损失函数也可以改写为:
重新组织一下常数,变为:
SVM 与 LR 的联系
到这里我们可以看出,SVM 的损失函数与 LR 的损失函数极为相似(LR 采用了 log loss $log(1+exp(-\gamma))$,而SVM采用了hinge loss $max(0, 1 - \gamma)$),二者的函数图像也很相似:
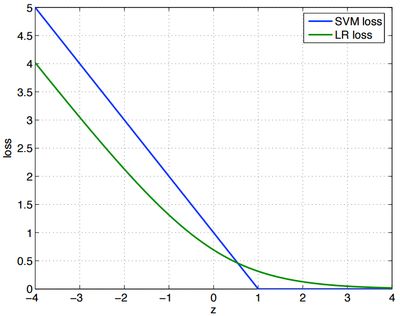
这两个损失函数的思想是一样的,也就是在预测正确而且确信度较大时($\gamma > 0$),loss 很小。而在预测错误而且错误的程度很大时,loss 与 $\gamma$ 成线性比例增加。实际上,二者在线性分类中取得的效果也是相似的。
在 SVM 的损失函数中,我们可以看出,对于分类正确的点,是没有loss的。因此只有那些距离分界面最近的点才对分界面有影响,这些点也称为支持向量。但是在 LR 中,分界面受所有数据点影响,只不过是分类正确的点影响比较小。
SVM 的另一个好处在于可以将其转换为对偶形式。在对偶形式下,整个损失函数只依赖于数据点间的内积,而不直接依赖数据本身,我们就可以采用核技巧来用 SVM 处理非线性问题。同时转化为对偶形式后,损失函数求解的复杂度也发生了变化(转化之前跟数据点的纬度有关,之后跟数据点的数量有关)。
LR 与 SVM 的求解以及对偶形式的转化在这里就不再详细展开了,网上有很多帖子。
逻辑回归与最大熵模型
最大熵模型
最大熵原理是统计学习的一般原理。我们假设分类模型学习一个条件概率分布 $p(y|x)$,这个分布不是随便来的,它应该满足一些特定的约束条件。对此我们可以定义一系列的特征函数 $f(x, y)$,注意这里的特征函数与一般情况不同,在一般情况下,我们只会考虑从输入中提取特征 $f(x)$,但 $f(x, y)$ 描述的是输入与输出之间的某一个事实,可以把它想象为用输入和输出同时来作特征提取。对提取出来的特征,我们可以计算其期望:
$p_{true}(x, y)$是数据和标记的真实分布,这个分布我们是不知道的,我们只能通过数据集来计算其经验分布:
当用我们模型的条件概率分布去替换掉上式中的经验条件概率分布时,我们可以得到特征函数关于模型的期望:
因此我们约束条件即为,这两个期望相等:
满足这个条件的分布可能有很多个,我们选取条件熵最大的那个,即我们的优化目标为:
通过对上式求解(拉格朗日乘子法,具体见这个教程) ,我们可以解得模型的一般形式:
这个形式跟逻辑回归已经非常相似了,如果在二分类问题中,我们定义特征函数如下:
这里的 $g(x)$ 才是我们通常情况下所说的特征函数,如 $x$ 是一段文本,我们提取它的 bag-of-words 特征作为特征向量。那么
这就是二分类逻辑回归, 详细的推理和讨论可以见这个回答.
特征函数
在一般情况中,我们通常只对输入进行特征提取,得到 $g(x)$,然后对于每个类别,都会有其自己的一套参数 $W^{(k)}$,通过二者内积,我们得到模型对于输入 $x$ 在类别 $y$ 下的置信程度。
关于特征函数 $f(x, y)$ 实际上是特征提取的另一种更加通用的视角。在这个视角下,我们可以对不同类别有针对性地提取不同的特征,最后组成 $NK$ 种特征,其中 $N$ 是单一类别提取特征的数量,$K$ 是类别数量。同时模型里还有 $NK$ 个参数与之相对应。
第二种特征提取方法在下面这种情况下于第一种等价: